Fibonacci-Zahlen: Was ist die goldene Spirale?

In der letzten Folge haben wir den Goldenen Schnitt behandelt, der als ideal schöne Proportion wichtig für Flächenaufteilungen im Grafik-Design ist. Doch bleibt der Goldene Schnitt in der Erinnerung eher abstrakt, weil es kein griffiges Bild für ihn gibt, das man verinnerlichen könnte. Die sogenannte Fibonacci-Zahlenfolge kann hier Abhilfe schaffen.

Wobei helfen Berechnungen im Medien-Design?

Der Goldene Schnitt und die Fibonacci-Folge kommen überall dort zum Einsatz, wo es um Proportionen geht:

Bei Seitenaufteilungen und Konstruktionen von Satzspiegeln für Bücher, Zeitschriften, Broschüren und Flyer
Bei Bildkomposition und Bildaufteilung in Fotografie und Illustration
Bei allem, was im Mediendesign an der Tagesordnung ist: von der Drucksache, über die Webseiten-Gestaltung bis zur Ausstellungsgestaltung.
Dabei vor allem auch für die Berechnung aller denkbaren Abstände und Größen für Seitenränder, Spaltenabstände oder Zeilenabstände sowie Bildgrößen und Bildproportionen
Es geht bei Abständen im Print-Design darum, in welchem Verhältnis der Weißraum einer Seite zur bedruckten Fläche steht

Die Berechnung der Schönheit

Der Goldene Schnitt ist spröde, da er unter Umständen mit schwierigen Berechnungen zu tun hat. Er bezeichnet das Verhältnis von zwei Teilen einer Strecke oder einer Fläche, wobei dieses Verhältnis ca. 1:1,618 entspricht. Genau das gilt als eine optimal schöne Proportion. Aber wie kann man es im Medien-Design gut handhabbar machen?

Die Fibonacci-Folge hilft, den Goldenen Schnitt zu verstehen

Der Goldene Schnitt hat einen mathematischen Verwandten, der hier helfen kann, auch weil er einprägsamer ist: Die Fibonacci-Folge ist benannt nach dem Italiener Leonardo Fibonacci. Der hatte damit, basierend auf antiken Rechenmethoden, bereits im Jahr 1202 die Fortpflanzungsrate von Kaninchen und das Pflanzenwachstum berechnet. Die Fibonacci-Folge wird durch die Fibonacci-Spirale visualisiert und ist dadurch bekannt geworden:

Die Goldene Spirale

Diese Goldene Spirale gibt damit einer Reihe aufsteigender Zahlen eine gut merkbare grafische Form. Die ist im übrigen auch Grundlage verschiedener Formen, die in der Natur vorkommen. Aber zunächst ist zu klären, was die Fibonacci-Zahlenfolge auszeichnet.

Die Fibonacci-Zahlen und ihre Besonderheit

Jede Zahlen-Sequenz ordnet Zahlen nach einer bestimmten Gesetzmäßigkeit an. Im Fall der Fibonacci-Folge ist jede Zahl (bis auf den Anfangswert) die Summe der zwei vorherigen. Die Zahlen steigen zwar am Anfang eher gemächlich an, dann aber entstehen sehr schnell immer größere Zahlen. So lautet die zwanzigste Fibonacci-Zahl bereits 4.181. Das ist der Grund, warum sich die Fibonacci-Spirale nach außen hin immer weiter öffnet. Die Additionen zu den ersten Zahlen der Fibonacci-Folge lauten beispielsweise:
0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13

Die Konstruktion der Fibonacci-Spirale

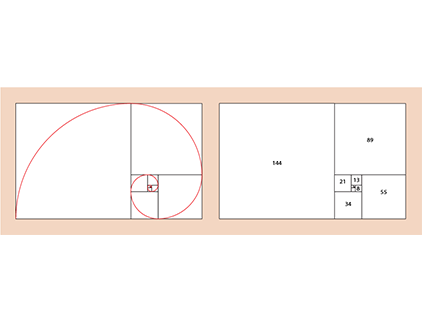Links oben: Die einzelnen Spiral-Segmente entstehen als Kreisbögen innerhalb von Quadraten. Rechts oben: In der Abbildung sind den Quadraten zur Verdeutlichung Zahlenwerte aus der Fibonacci-Folge zugeordnet.

Goldene Proportionen

Links oben: Wenn man die Darstellung weiter vereinfacht, ergibt sich ein Quadrat mit einem Rechteck daneben, das in anderen Fällen auch über oder unter dem Quadrat liegen kann. Das Ensemble aus Quadrat und Rechteck hat nahezu die gleichen Verhältnis-Werte wie der Goldene Schnitt. Allerdings sind die Fibonacci-Zahlen am Anfang, in ihren kleineren Zahlenwerten, noch weit entfernt vom Goldenen Schnitt. Je weiter sie jedoch fortschreiten und je größer sie werden, desto mehr nähern sie sich dem Verhältnis von 1:1,618 an. Genauer gesagt: Die Division zweier aufeinanderfolgender Werte nähert sich der Goldenen Proportion an. Beispielsweise ist 3 : 2 = 1,5 noch weit weg vom idealen Verhältnis. 13 : 8 = 1,625 nähert sich dem aber schon an und 55 : 34 = 1,617 kommt dem Goldenen Schnitt schon sehr nahe. Es ist aber nicht so, dass mit weiterem Steigen der Werte, der Goldene Schnitt genau erreicht wird. Vielmehr wechselt die Annäherung: sie liegt einmal knapp unter dem Goldenen Zahlenverhältnis, dann wieder darüber. Der Laie, der die Zahlen anwenden möchte, kann daraus aber dennoch den Schluss für die Praxis ziehen, dass die Fibonacci-Zahlen, die ein mathematisches Wachstum beschreiben, dem Goldenen Schnitt ungefähr nahe kommen.

Was ist der Vorteil der Fibonacci-Folge?

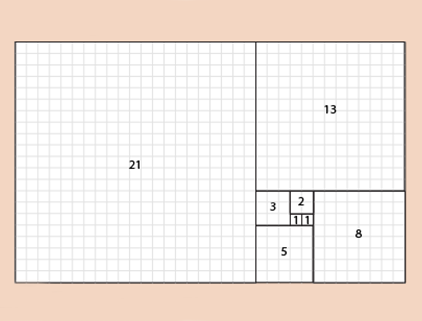
Fibonacci-Zahlen lassen sich besser rechnen. Dies wird an folgendem Beispiel anschaulicher:

Hier ist ein quadratisches Raster hinterlegt, das zeigt, dass sich die Fibonacci-Proportionsverhältnisse wohl geordnet aufeinander beziehen. Dabei bildet die Grundproportion immer ein großes Quadrat (hier im Bild links für die Fibonacci-Zahl 21) mit zugeordnetem Rechteck (das aus den restlichen Quadraten der Zahlen 13 bis 1 gebildet wird). Die Fibonacci-Zahl 13 wiederum bildet das nächstkleinere Quadrat, dem das Rechteck zusammengesetzt aus den Quadraten der Zahlen 8 bis 1 zugeordnet ist. Grundlegend ist immer eine selbstähnliche Struktur, die aus Quadrat und Rechteck gebildet wird.

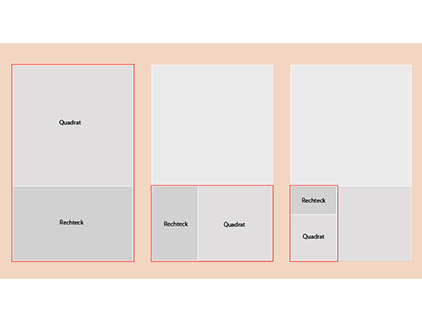Das Verhältnis zwischen Quadrat und Rechteck entspricht dabei nahezu dem Goldenen Schnitt. Der Goldene Schnitt ist mathematisch betrachtet jedoch eine sogenannte irrationale Zahl, die sich nicht als Bruchzahl darstellen lässt. Deshalb lässt sich der Goldene Schnitt zwar (siehe Folge 2 dieser Serie) berechnen, er ist für den Designer aber weniger einfach handhabbar. Fibonacci-Zahlen sind übersichtlich und besser in die Welt des Designs übertragbar.

Konstruktion des Goldenen Schnitts

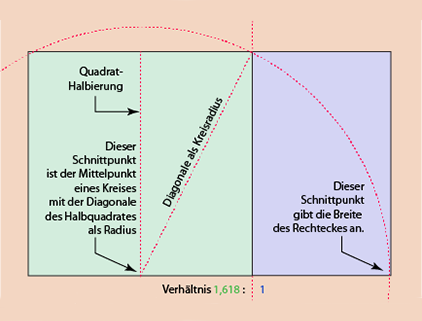
Der Goldene Schnitt lässt sich allerdings rein grafisch ohne Berechnung recht einfach konstruieren. Es gibt viele Möglichkeiten, eine davon ist nachfolgend abgebildet:

Dabei geht man von einem beliebigen Quadrat aus (hier grün dargestellt).

Das Quadrat wird zunächst halbiert (rot-gestrichelte, vertikal verlaufende Hilfslinie).
Der Schnittpunkt, der sich mit der unten liegenden Seite des Quadrates und der Halbierungslinie ergibt, ist der Mittelpunkt eines gedachten Kreises.
Der Radius des gedachten Kreises ist die Diagonale des halbierten Quadrates (rot-gestrichelte, schräg verlaufende Hilfslinie).
Wendet man den Kreis auf dieser Grundlage an, bildet er einen Schnittpunkt mit der verlängerten unteren Linie des Quadrates. Dieser gibt die Breite des Rechteckes an, das nun zum Quadrat im Verhältnis 1,618 : 1 steht.

Fazit: Proportionen einfach oder kompliziert

Der Begriff „Goldener Schnitt“ hört sich einfach und klar an, kann aber kompliziert werden. Fast jede aussagekräftige Quelle im Internet benutzt zur Berechnung des Goldenen Schnittes schnell Formeln, die man als Nicht-Mathematiker kaum versteht. Dabei ist es noch relativ einfach, eine Strecke im Verhältnis 1 : 1,618 zu teilen. Angewendet auf die komplexen Flächenaufteilungen einer Drucksache wird es komplizierter. Das hängt unter anderem damit zusammen, dass unsere DIN-Formate stark vom Goldenen Schnitt abweichen. Manch ein Designer fragt sich dann, wie er mit dieser Einschränkung überhaupt arbeiten kann. Mehr dazu in der nächsten und letzten Folge der Serie.

Der Begriff „Fibonacci“ hört sich dem gegenüber kompliziert an, ist aber für den Laien transparenter und einfacher in der Anwendung. Die Fibonnaci-Folge kann man als eine für den Einsteiger besser verstehbare Entsprechung zum Goldenen Schnitt auffassen.

Sie arbeitet mit ganzen Zahlen (und nicht mit Dezimalzahlen mit vielen Nachkommastellen), mit denen man komplette Satzspiegel schlüssig erstellen kann – und zwar ohne große Berechnungen, sondern mit einem Rastersystem, das auf den Fibonacci-Zahlen basiert.

Die Arbeit mit solchen Rastersystemen vereinfacht es, umfangreiche Drucksachen wie Magazine oder Kataloge zu vereinheitlichen. Auch Printprodukte, die in Reihen erscheinen, profitieren von der flexiblen Durchgängigkeit der Gestaltungsraster. Ein Raster für zum Beispiel 20 Flyer, die nach und nach in einer Serie erscheinen, sichert in Proportionen und Fotogrößen deren grundlegende Wiedererkennbarkeit.

Es sei noch erwähnt, dass die berühmte Zahl „Phi“, in mathematischer Symbolsprache auch „φ“ geschrieben, genau den Wert 1,61803399 hat und damit dem Goldenen Schnitt entspricht. Deshalb wird die Zahl „Phi“ auch „Goldene Zahl“ genannt.